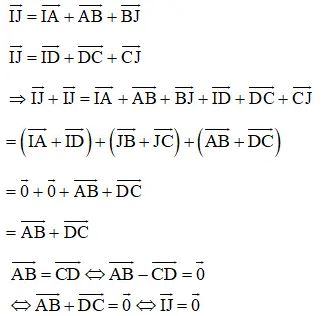Tóm tắt kiến thức toán hình lớp 10 bài 2: Tổng và hiệu của hai vectơ
Tóm tắt kiến thức hình lớp 10 bài 2: Tổng và hiệu của hai vectơ
Mục lục
Dưới đây là bài tóm tắt kiến thức và hướng dẫn giải toán hình lớp 10 bài 2: Tổng và hiệu của hai vectơ, mà các bạn có thể tham khảo để học tốt hơn!
Tóm tắt kiến thức toán hình lớp 10 bài 2
Với bài này, các bạn cần nắm được các nội dung sau
I – TỔNG CỦA HAI VECTƠ
- Định nghĩa:
Cho hai vectơ và . Lấy một điểm A tùy ý, vẽ = và BC = . Vectơ
được gọi là tổng của hai vectơ và .
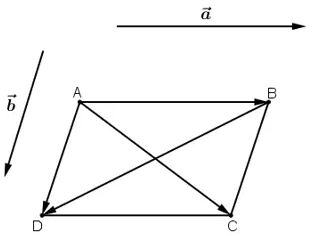
II – QUY TẮC HÌNH BÌNH HÀNH
- Nếu ABCD là hình bình hành thì
+
=
III – TÍNH CHẤT CỦA PHÉP CỘNG CÁC VECTƠ
Với ba vectơ , , tùy ý ta có:
- Tính chất giao hoán:
+ = +
- Tính chất kết hợp:
( + ) += + ( +
)
- Tính chất của vectơ – không:
+ =
+ =
IV – HIỆU CỦA HAI VECTƠ
- Định nghĩa:
Cho hai vectơ và . Ta gọi hiệu của hai vectơ và là vectơ + (-)
Kí hiệu: –
- Vectơ đối:
Cho vectơ . Vectơ có cùng độ dài và ngược hướng với được gọi là vectơ đối của .
Kí hiệu: –
Hướng dẫn giải bài tập toán hình lớp 10 bài 2
Bài tập trong sách: (sgk/12)
Câu 1:
Cho đoạn thẳng AB và điểm M nằm giữa A và B sao cho AM > MB. Vẽ các vectơ +
và
–
.
Lời giải:
Trên đoạn MA, lấy điểm C sao cho MC = MB
Nhận thấy và
cùng hướng nên
=
Khi đó:
+
=
+
= +
=
–
=
Câu 2:
Cho hình bình hành ABCD và một điểm M tùy ý, Chứng minh rằng +
=
+
.
Lời giải:
Ta có ABCD là hình bình hành nên =
+
=
+
+
+
= ( +
) + (
+
)
= ( +
) + (
+
) ( Vì
=
)
= ( +
) + 0
= +
(đpcm)
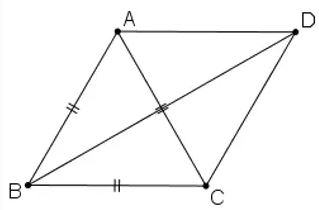
Câu 3:
Chứng minh rằng đối với tứ giác ABCD bất kì ta luôn có:
a) +
+
+
=
b)
–
=
–
Lời giải:
a) Ta có:
+
+
+
= ( +
) + (
+
)
= +
= =
b) Áp dụng quy tắc trừ hai vectơ ta có:
–
=
–
=
Do đó:
–
=
–
(đpcm)
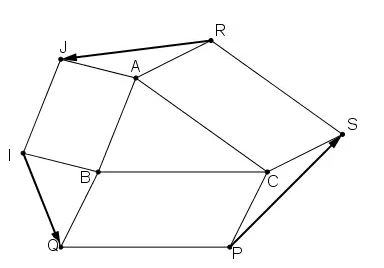
Câu 4:
Cho tam giác ABC. Bên ngoài của tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS. Chúng minh rằng +
+
=
Lời giải:
Ta có: AJIB là hình bình hành nên: =
⇒ +
=
+
=
=
BCPQ là hình bình hành nên: +
=
CARS là hình bình hành nên: +
=
Do đó:
+
+
= ( +
) + (
+
) + (
+
)
= ( +
) + (
+
) + (
+
)
= +
+
=
(đpcm)
Câu 5:
Cho tam giác đều ABC cạnh bằng a. Tính độ dài của các vectơ +
và
–
.
Lời giải:
Cho D là điểm đối xứng của B qua AC. Ta có hình bình hành ABCD:
Ta có: +
=
Do đó ∣ +
∣ = ∣
∣ = AC = a
Ta có: –
=
+
=
(Quy tắc hình bình hành)
Do đó: ∣ –
∣ = ∣
∣ = BD
Gọi O là giao điểm của AC và BD
Ta có: AO = AC/2 = a/2
⇒ BO = √(AB2 – AO2) (định lý pytago)
= √(a2 – (a/2)2)
= (a√3)/2
⇒ BD = 2BO = a√3
Vậy ∣ –
∣ = a√3
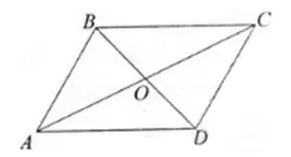
Câu 6:
Cho hình bình hành ABCD có tâm O. Chứng minh rằng
a) –
=
; b)
–
=
;
c) –
=
–
; d)
–
+
=
Lời giải:
a) Ta có:
O là trung điểm của AC nên =
Do đó: –
=
–
=
(đpcm)
b) ABCD là hình bình hành nên =
Do đó: –
=
–
=
c) Ta có:
–
=
–
=
Mà ABCD là hbh nên =
Do đó: –
=
–
(đpcm)
d) Ta có:
ABCD là hbh nên =
–
=
Do đó: –
+
=
–
=
=
(đpcm)
Câu 7:
Cho , là hai vectơ khác. Khi nào có đẳng thức:
a)| + |=||+||; b)| + |=| – |
Lời giải:
Vẽ hình bình hành ABCD sao cho = ,
=
Ta có:
| + |= | +
|=|
|= AC
| – |=| –
|=|
|= BD
||=||= AB , ||=|
|= AD = BC
Do đó:
a)| + |=||+||⇔ B nằm giữa A và C ⇔ và
cùng hướng hay và cùng hướng.
b)| + |=| – |⇔ ABCD là hình chữ nhật ⇔ AB ⊥ CD hay ⊥ .
Câu 8:
Cho| + |= 0 . So sánh độ dài, phương và hướng của hai vectơ và .
Lời giải:
| + |= 0 ⇔ + =⇔ = –
⇔ và là hai vectơ đối nhau
⇔ và cùng phương, ngược hướng và có cùng độ dài.
Câu 9:
Chứng minh rằng =
khi và chỉ khi trung điểm của hai đoạn thẳng AD và DC trùng nhau.
Lời giải:
Gọi I trung điểm của AD, J là trung điểm của BC.
Ta có:
+
=
,
+
=
Theo quy tắc ba điểm ta có:
⇔ I J hay trung điểm AD và BC trùng nhau (đpcm)
Đó là tóm tắt kiến thức và hướng dẫn giải toán hình lớp 10 bài 2: Tổng và hiệu của hai vectơ, các bạn có thể tham khảo. Đừng quên xem thêm các bài giải toán khác tại chuyên mục : Toán Học lớp 10 .
We on social :