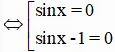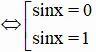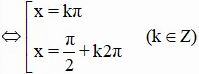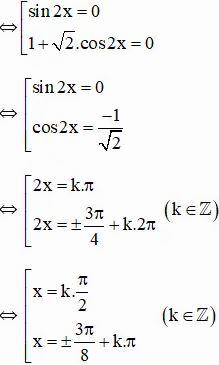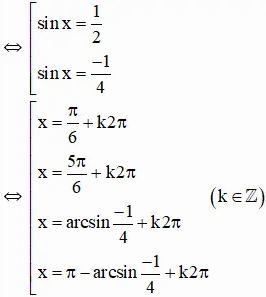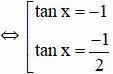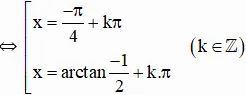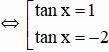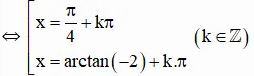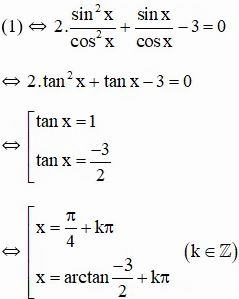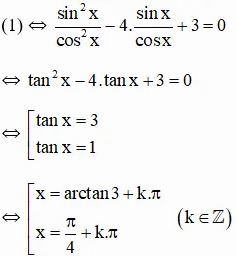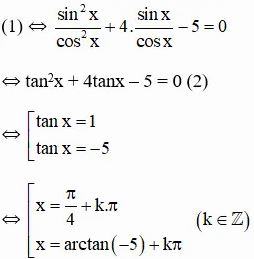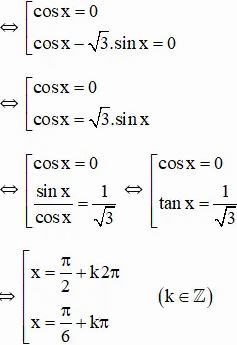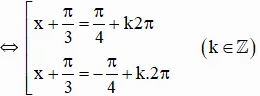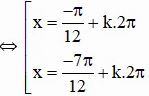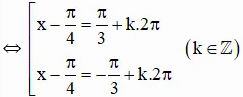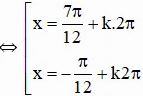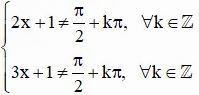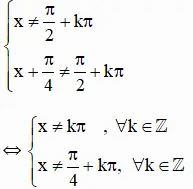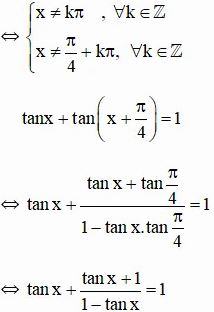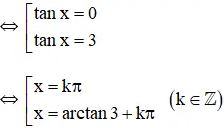Tóm tắt kiến thức toán lớp 11 bài 3: Một số phương trình lượng giác thường gặp

Dưới đây là bài tóm tắt kiến thức và hướng dẫn giải toán lớp 11 bài 3: Một số phương trình lượng giác thường gặp, mà các bạn có thể tham khảo để học tốt hơn!

Tóm tắt kiến thức toán lớp 11 bài 3

Với bài này, các bạn cần nắm được các nội dung sau 

I – PHƯƠNG TRÌNH BẬC NHẤT ĐỐI VỚI MỘT HÀM SỐ LƯỢNG GIÁC

 Định nghĩa:

 Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng

at + b = 0

trong đó a, b là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.

II – PHƯƠNG TRÌNH BẬC HAI ĐỐI VỚI MỘT HÀM SỐ LƯỢNG GIÁC

 Định nghĩa:

 Phương trình bậc hai đối với một hàm số lượng giác là phương trình có dạng

at² + bt + c = 0

trong đó a, b, c là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.

III – PHƯƠNG TRÌNH BẬC HAI ĐỐI VỚI sinx VÀ cosx

1. Công thức biến đổi biểu thức asinx + bcosx

asinx + bcosx = sin(x + a),

với cosa = và sina =

2. Phương trình dạng asinx + bcosx = c

Nếu a = 0, b ≠ 0 hoặc a ≠ 0, b = 0, phương trình asinx + bcosx = 0 có thể đưa quay về phương trình lượng giác cơ bản. Nếu a ≠ 0, b ≠ 0, ta áp dụng công thức asinx + bcosx = sin(x + a)

 

Hướng dẫn giải bài tập toán lớp 11 bài 3

Bài tập trong sách: (sgk/36)

Câu 1: Giải phương trình:

                                  sin2x – sinx = 0

Lời giải:

      sin²x – sinx = 0

⇔ sinx(sinx – 1) = 0

Vậy phương trình có tập nghiệm {kπ ; π/2 + k2π} (k ∈ Z)

Câu 2: Giải các phương trình sau:

a) 2cos²x – 3cosx + 1 = 0                        b) 2sin2x + √2.sin4x = 0

Lời giải:

a) 2cos²x – 3cosx + 1 = 0

Đặt t = cosx, ĐK: -1 ≤ t ≤ 1

Thay t vào phương trình, ta có:

        2t² + 3t + 1 = 0

⇔ t = 1 và t = 1/2   (thỏa ĐK)

Khi t = 1 ⇒ cosx = 1 ⇔ x = k2π (k ∈ Z)

Khi t = 1/2 ⇒ cosx = 1/2 

⇔ cosx = cosπ/3

⇔ x = ± π/3 + k2π (k ∈ Z)

Vậy phương trình có tập nghiệm {k2π ; ± π/3 + k2π} (k ∈ Z)

b) 2sin2x + √2.sin4x = 0

⇔ 2sin2x + 2√2.sin2x.cos2x = 0

⇔ 2sin2x (1 + √2.cos2x) = 0

Vậy phương trình có tập nghiệm {kπ/2 ; ± 3π/8 + kπ} (k ∈ Z)

Câu 3: Giải các phương trình sau:

a) sin²(x/2) – 2cosx/2 + 2 = 0 ; b) 8cos²x + 2sinx + 7 = 0 ;

c) 2tan²x + 3tanx + 1 = 0 ;                     d) tanx – 2cotx + 1 = 0.

Lời giải: 

a) sin²(x/2) – 2cosx/2 + 2 = 0

⇔ (1 – cos²(x/2)) – 2cosx/2 + 2 = 0

⇔ – cos²(x/2) – 2cosx/2 + 3 = 0

⇔ cos²(x/2) + 2cosx/2 – 3 = 0 (Pt bậc hai với ẩn cosx/2)

⇔ cosx = 1 (nhận) và cosx = -3 (loại)

⇔ x = kπ (k ∈ Z)

Vậy phương trình có tập nghiệm {x = kπ} (k ∈ Z)

b) 8cos²x + 2sinx + 7 = 0

⇔ 8(1 – sin²x) + 2sinx + 7 = 0

⇔ 8sin²x – 2sinx – 1 = 0 (Pt bậc hai với ẩn sinx)

Vậy phương trình có tập nghiệm {π/6 + k2π; 5π/6 + k2π; arcsin(-¼) + k2π; π – arcsin(-¼) + k2π} (k ∈ Z)

c) 2tan²x + 3tanx + 1 = 0 (ĐK: x ≠ π/2 + kπ)

Vậy phương trình có tập nghiệm {-π/4 + kπ; arctan(-½) + kπ} (k ∈ Z)

d) tanx – 2cotx + 1 = 0 (ĐK: )

⇔ tanx – 2.1/tanx + 1 = 0

⇔ tan²x – 2 + tanx = 0

⇔ tan²x + tanx – 2 = 0

Vậy phương trình có tập nghiệm {π/4 + kπ; arctan(-2) + kπ} (k ∈ Z)

Câu 4: Giải các phương trình sau:

a) 2sin²x – sincosx – 3cos²x = 0 ;

b) 3sin²x – 4sincosx + 5cos²x = 2 ;

c) sin²x + sin2x – 2cos²x = 1/2 ;

d) 2cos²x – 3√3 sin2x – 4sin²x = -4

Lời giải: 

a) 2sin²x – sincosx – 3cos²x = 0     (1)

• TH1: cosx = 0 ⇒ sin²x = 1 – cos²x = 1

Phương trình (1) trở thành: 2 = 0 (loại)

• TH2: cosx ≠ 0, chia cả hai vế của (1) cho cos²x ta được:

Vậy phương trình có tập nghiệm {π/4 + kπ; arctan(-3/2) + kπ} (k ∈ Z)

b) 3sin²x – 4sincosx + 5cos²x = 2

⇔ 3sin²x – 4sinx.cosx + 5cos²x = 2(sin²x + cos²x)

⇔ sin²x – 4sinx.cosx + 3cos²x = 0   (1)

• TH1: cosx = 0 ⇒ sin²x = 0

Phương trình (1) trở thành: 1 = 0 (loại)

• TH2: cosx ≠ 0, chia cả hai vế của (1) cho cos²x ta được:

Vậy phương trình có tập nghiệm {arctan3 + kπ; π/4 + kπ; } (k ∈ Z)

c) sin²x + sin2x – 2cos²x = ½

⇔ sin²x + 2sinxcosx – 2cos²x = ½(sin²x + cos²x)

⇔ 1/2sin²x + 2sinxcosx – 5/2cos²x = 0

⇔ sin²x + 4sinxcosx – 5cos²x = 0    (1)

• TH1: cosx = 0 ⇒ sin²x = 1 – cos²x = 1

Phương trình (1) trở thành: 1 = 0 (loại)

• TH2: cosx ≠ 0, chia cả hai vế của (1) cho cos²x ta được:

Vậy phương trình có tập nghiệm {π/4 + kπ; arctan(-5) + kπ} (k ∈ Z)

d) 2cos²x – 3√3 sin2x – sin²x = -4

⇔ 2cos²x – 3√3.2sinxcosx – 4sin²x = -4(sin²x + cos²x)

⇔ 6cos²x – 6√3.sinxcosx = 0

⇔ 6cosx – (cosx – √3.sinx) = 0

Vậy phương trình có tập nghiệm {π/2 + k2π; π/6 + kπ} (k ∈ Z)

Câu 5: Giải các phương trình sau:

a) cosx – √3 sinx = √2 ;                         b) 3sin3x – 4cos3x = 5 ;

c) 2sinx + 2cosx – √2 = 0 ;                    d) 5cos2x + 12sin2x – 13 = 0.

Lời giải: 

a) cosx – √3 sinx = √2

⇔ ½.cosx – (√3)/2 . sinx = 1/√2

⇔ cos(π/3)cosx – sin(π/3)sinx = 1/√2

⇔ cos(π/3 + x) = cos(π/4)

Vậy phương trình có tập nghiệm {-π/12 + k2π; -7π/12 + k2π} (k ∈ Z)

b) 3sin3x – 4cos3x = 5

⇔ (⅗)sin3x – (⅘)cos3x = 1    (1)

Ta có (3/5)² + (4/5)² = 1 nên tồn tại α thỏa cosα = 3/5 và sinα = 4/5

(1) ⇔ cosα.sin3x – sinα.cos3x = 1

⇔ sin(3x – α) = 1

⇔ 3x – α = π/2 + k2π  (k ∈ Z)

⇔ 3x = α + π/2 + k2π

⇔ x = ∝/3 + π/6 + k2π/3

Vậy phương trình có tập nghiệm x = ∝/3 + π/6 + k2π/3 (k ∈ Z)

c) 2sinx + 2cosx – √2 = 0

⇔ 2sinx + 2cosx = √2

⇔ cosx(1/√2) + sinx(1/√2) = 1/2

⇔ cosx.cos(π/4) + sinx.sin(π/4) = ½

⇔ cos(x – π/4) = cos(π/3)

Vậy phương trình có tập nghiệm {7π/12 + k2π; -π/12 + k2π} (k ∈ Z)

d) 5cos2x + 12sin2x – 13 = 0

⇔ 5cos2x + 12sin2x = 13

⇔ (5/13)cos2x + (12/13)sin2x = 1     (1)

Ta có (5/13)² + (12/13)² = 1 nên tồn tại α thỏa cosα = 5/13 và sinα = 12/13

(1) ⇔ cosα.cos2x + sinα.sin2x = 1

⇔ cos(2x – α) = 1

⇔ 2x – α = k2π (k ∈ Z)

⇔ 2x = α + k2π

⇔ x = -α/2 + kπ

Vậy phương trình có tập nghiệm x = -α/2 + kπ (k ∈ Z)

Câu 6: Giải các phương trình sau:

a) tan(2x + 1)tan(3x – 1) = 1 ;               b) tanx + tan(x + π/4) = 1 

Lời giải: 

a) tan(2x + 1)tan(3x – 1) = 1 

ĐK:

⇒ tan(2x + 1) = 1/tan(3x – 1)

⇔ tan(2x + 1) = cot(3x – 1)

⇔ tan(2x + 1) = tan(π/2 – 3x + 1)

⇔ 2x + 1 = π/2 – 3x + 1 + kπ (k ∈ Z)

⇔ 5x = π/2 + kπ

⇔ x = π/10 + kπ/5  (nhận)

Vậy phương trình có tập nghiệm x = π/10 + kπ/5 (k ∈ Z)

b) tanx + tan(x + π/4) = 1

ĐK:

⇔ tanx(1 – tanx) + tanx +1 = 1 – tanx

⇔ tanx – tan²x + 2tanx = 0

⇔ tan²x + 3tanx = 0

⇔ tanx(tanx – 3) = 0

Vậy phương trình có tập nghiệm {kπ; arctan3 + kπ} (k ∈ Z)

 

Đó là tóm tắt kiến thức và hướng dẫn giải toán lớp 11 bài 3: Một số phương trình lượng giác thường gặp, các bạn có thể tham khảo. Đừng quên xem thêm các bài giải toán khác tại chuyên mục : Toán Học lớp 11 .

We on social :

Facebook